You are given n non-negative integers a1, a2, , an. In a single operation, you take any two integers out of these integers and replace them with a new integer having value equal to difference between those integers ie, if the removed integers are b and c, you put |b — c| into the set again. You keep applying the operation until you are left with only a single number, So After n — 1 steps the game will terminate, you need to find out what is maximum value of the single number left in the end after n — 1 such operations.
I am interested in seeing any polynomial time algorithm for the problem, Currently I dont have any idea about how to solve this problem less than 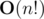 .
.
If you feel that there does not any polynomial time algorithm, could you please establish in which complexity class it lies, Is it NP complete ?











One observation is that if you fix the last number you are subtracting from, then for the rest of the numbers you just need to minimize the result of their subtraction. Unless I miss something this can be treated as Partition optimization problem. That is still NP-complete, but depending on the max value of a[i] you can try applying knapsack-like dynamic programming approach.
I really did not understood that how you can treat it partition problem, because here problem is that the bracketting order matters, so it can not be framed directly like find two partitions with equal sum. I was thinking of dynamic programming approach too, but I really did not know what should be the order of the elements to take?
What do you mean by bracketing? Is there a restriction that you can subtract only numbers standing next to each other? Otherwise if you have a set of numbers and you need to assign +/- to each number and minimize the total sum, then I would say that you would be able to get that sum by using the actions you described.
Example:
Numbers: 7 5 3 3 6 6
Let's say you want to make it into this: +7 +5 +3 -3 -6 -6. The total sum will be 0, which is optimal. So I'm saying (though I have no proof for it) that you will be able to achieve in this way (highlighted in bold are the numbers which will be subtracted):
7 5 3 3 6 6
1 5 3 3 6
5 5 3 3
0 3 3
3 3
0
So I've got zero in this particular case. This way you will be able to get any partition sum, if it optimal. You might be unable to reach non-optimal sums using your operations, but you don't care about non-optimal solutions. For example let's take numbers 7 and 5. You can achieve the following partial sums: 0, 5, 7, 12. Out of those you won't be able to get 0 and 12 using abs/minus operations, but you don't care about that because 0 and 12 won't give an optimal answer anyway.
the question asks for maximum value of answer, not minimum!
As marat.snowbear said, if you fix the element you want to use on the last step to get maximum result, you have to find minimum value for other numbers. And even this isn't the whole problem as the best solution may be like "use a and b and keep the result |a - b| for the last step".
I'm pretty sure and have some sketch of the proof (enough to convince myself) that optimal solution (or at least one of them if there are many) can be composed by taking some of the original values (without combining it with any other value) at the last step and subtracting a combination of other values from it.
I also suppose that it might be a case that this value used on the last step is always the maximum one from the original set but I have no proof of it.
For the part you said that you dont have a proof, I think that is the most important step in proving the problem to be lying in some complexity class or being equivalent to some previously known NP hard problem.
As far as I understand, Even a given expression with given numbers with + and — signs, it is not even easy to check whether some arrangement of actual operations on the array could give this expression or not?
P.S. By bracketting, I kind of losely meant that the actual substraction order you need to do, the one that you described using numbers in bold, Though I admit that bracketting was not a good word to use there :(
what do you mean by "arrangement of actual operations"? Do you mean like if you have expression like "5 + 4 — 2 + 6" then this arrangement is in which order you do the operations? Like in my example whether you first add "5 + 4" or you subtract "4 — 2" or you add "2 + 6"?
By Arrangement of Actual operations, I mean following.
An expression is a combinations of series of + and — followed by integers from the array a. eg. a = [7 5 3 3 6 6] Then one of the expressions is : +7 +5 +3 -3 -6 -6.
An expression is valid if it actually corresponds to application of some operations in the array. eg. The above given expression is valid because we can obtain this expression using operations from the array as given in your previous to previous comment.
Now example of an invalid expression: a = [1,2,3] Then expression + 1 + 2 — 3 is invalid, Because you can never apply actual operations in the way such that largest value is negative.
Note that if the largest value in some expression is negative, then the expression is always invalid. There are also some other ways when the the expressions are invalid. One way of seeing this is that there are many ways of making expressions which evaluate more than the largest value in the array a, All of those expressions are invalid because we know that our final result should be <= largest value in the array.
Note that there are still many expression other above mentioned that which are also invalid. For now I dont have any algorithm to determine whether the given expression is valid or not?. I feel like that this is main difficult part of the algorithm.
I hope the phrase "arrangement of actual operations" makes sense now, For your given expression 5 + 4 — 2 + 6 is invalid because there is no actual series of operations on the array, which leads to this arrangement.
Eg. (6 — (2 — (5 — 4)) gives you 6 — 2 + 5 — 4.
(6 — (5 — (4 — 2)) gives you 6 — 5 + 4 — 2.
But note that (6 — ((4 — 2) — 5)) is invalid expression because (4 — 2) — 5 gives you negative value which is not allowed, because we are always replacing by |b — c|.
By the previous examples you can see that 6 — 2 + 5 — 4 and 6 — 5 + 4 — 2 are valid expressions.
==============================================================================================
As I said before you don't need to worry about this one being invalid because it won't be optimal anyway. You will get better (smaller abs value) result by subtracting any one of (5, 4 or 6). So I think you can safely use the algorithm I proposed because results which are invalid will never be optimal.
You can treat it like that but I think it's easier not to care about the actual sign of the result and try to optimize the absolute value. From this point of view "1 + 2 — 3" is equal to "-1 -2 +3" which is valid in your terms.
The entire idea is as follows. Let's say you have separated your set into two sets: those which we're showing with positive sign and those which will be negative. Let's also have some accumulator which will contain currently accumulated result of adding/subtracting the items. We allow this accumulator to be negative as well as positive. For your goal you care only about its absolute value so having a sign will not hurt if you do all the operations correctly. So we have this accumulator initialized as zero and we're going to apply all numbers from both sets to it. On each step we're going to apply exactly one number from either positive or negative set to the accumulator. The idea is if at the moment your accumulator is positive then you apply numbers from negative set, if accumulator is negative then you apply any number from positive set. Now you need to verify two things:
Given two sets, whether you will be able to apply all the numbers from them according to your rules.
Whether the result you will achieve (the absolute value of the accumulator after applying all the numbers) is equal to the result you would achieve by applying your actual rules to the numbers in the same order. You can convince yourself this is true because of the way we always select numbers to be applied from the "opposite" set.
So let's try to prove the first statement. Let's say we have applied some numbers already and we have some accumulator value and we have two sets. I will call those sets "this set" and "opposite set". "This set" is the set with same sign as accumulator. "Opposite" set is another one. So when we're going to apply next number we might have different cases:
This set is empty and that set is empty. That means we applied all the numbers and achieved the result.
Opposite set is empty but this set has some numbers. This means that you won't be actually able to apply numbers anymore according to your rule. But if you think about this case you will see that this is obviously non-optimal solution. Because if for example your accumulator is positive then it makes absolutely no sense to add any more numbers to it, you might want to subtract numbers instead. That's why I'm saying that impossible solutions are non-optimal. Because they are non-optimal you don't need to care whether they are valid or not, you will find better solution anyway.
Opposite set has some numbers. In this case you just apply the number from the opposite set and repeat this operations.
This way I convinced myself that solving partition optimization problem will actually solve your problem.
I am convinced in your arguments of this problem being reduced to partition problem.
I also posted the question to Mathoverflow too because I thought the finding which complexity class lies outside of the codeforces domain. There it had been proved that problem is indeed NP-Hard. You might be interested in link http://mathoverflow.net/questions/160813/an-interesting-optimization-problem.
For really small constraints, like N ≤ 20 and Ai ≤ 100, it can be solved with DP, where the state is DP[m][k]. m is the bitmask that indicates which numbers have been taken and k is the number that remains after taking all those numbers. Every element in DP is a boolean. Then the answer is the maximum k such that DP[2N - 1][k] is true.
But, of course, that will work only with VERY small constraints.
EDIT: It won't work at all, hadn't read problem statement very well...
I had thought about this approach, but I believe that this is incorrect !!