Для решения задачи важно заметить, что в ходе игры количество монет на столе меняться не может. Суммарное количество монет на столе после того, как сделаны ставки, остается неизменным. Следовательно, разделив суммарное количество монет на столе на количество игроков, можно получить начальную ставку каждого из них. Если разделить без остатка невозможно, то такой итог игры невозможен. Стоит обратить внимание на то, что начальная ставка каждого из игроков должна быть отлична от нуля, следовательно, ноль никогда не может являться ответом.
Если переформулировать задачу в терминах теории графов, то ее можно сформулировать следующим образом: Имеется граф, состоящий из n вершин и m компонент связности. Внутри каждой компоненты связности каждая пара вершин этой компоненты связана ребром. Другими словами, каждая компонента связности является полносвязной. Какое наименьшее и какое наибольшее количество ребер может содержать такой граф? Рассмотрим процесс построения графа из n вершин и m компонент связности. Для начала предположим, что каждая из m компонент содержит ровно одну вершину. Остается распределить оставшиеся n - m вершин так, чтобы минимизировать или максимизировать количество ребер. Заметим, что при добавлении новой вершины в компоненту связности размера k, количество ребер увеличивается на k (новая вершина соединяется с каждой из уже существующих одним ребром). Следовательно, для того, чтобы минимизировать количество образованных ребер на каждом шаге, требуется каждый раз добавлять вершину в компоненту связности наименьшего размера. Если действовать согласно такой стратегии, то после распределения вершин по компонентам связности появится 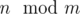 компонент размера
компонент размера 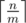 и
и 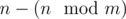 компонент размера
компонент размера 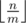 . Аналогично, для того, чтобы максимизировать количество ребер, на каждом шаге необходимо добавлять очередную вершину в компонентну связности наибольшего размера. Если действовать согласно такой стратегии, то образуется одна компонента связности размера n - m + 1, оставшиеся компоненты связности будут состоять из одной вершины. Зная количество компонент связности и их размеры, можно посчитать общее количество ребер. Для полносвязной компоненты, состоящей из k вершин, количество ребер равняется
. Аналогично, для того, чтобы максимизировать количество ребер, на каждом шаге необходимо добавлять очередную вершину в компонентну связности наибольшего размера. Если действовать согласно такой стратегии, то образуется одна компонента связности размера n - m + 1, оставшиеся компоненты связности будут состоять из одной вершины. Зная количество компонент связности и их размеры, можно посчитать общее количество ребер. Для полносвязной компоненты, состоящей из k вершин, количество ребер равняется 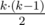 . Следует помнить про необходимость использовать 64-битный тип данных для хранения количества ребер, которое квадратично зависит от значения n.
. Следует помнить про необходимость использовать 64-битный тип данных для хранения количества ребер, которое квадратично зависит от значения n.
Рассмотрим ситуацию, когда величина max(r, g, b) - min(r, g, b) ≤ 1, в таком случае, очевидно, ответ равен 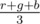 . Мы всегда можем украсить столько столов тремя воздушными шарами разных цветов. Очевидно, что оставшееся количество шаров будет меньше трех и, следовательно, не может быть использовано для украшения стола в любом случае. Все оставшиеся случаи имеет смысл свести к ранее рассмотренному. Если есть один цвет такой, что количество шариков этого цвета больше, чем суммарное количество шариков для оставшихся двух цветов, то всега выгодно украшать стол двумя шарами этого цвета и одним шаром того из оставшихся цветов, которого больше на данный момент. Далее можно разными способами группировать операции и выполнять более одной операции за раз. Другим решением можно назвать тот факт, что ответ будет отличен от
. Мы всегда можем украсить столько столов тремя воздушными шарами разных цветов. Очевидно, что оставшееся количество шаров будет меньше трех и, следовательно, не может быть использовано для украшения стола в любом случае. Все оставшиеся случаи имеет смысл свести к ранее рассмотренному. Если есть один цвет такой, что количество шариков этого цвета больше, чем суммарное количество шариков для оставшихся двух цветов, то всега выгодно украшать стол двумя шарами этого цвета и одним шаром того из оставшихся цветов, которого больше на данный момент. Далее можно разными способами группировать операции и выполнять более одной операции за раз. Другим решением можно назвать тот факт, что ответ будет отличен от 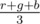 , но только тогда, когда max(r, g, b) ≥ 2·(r + g + b - max(r, g, b)), в таком случае ответ r + g + b - max(r, g, b). В этом случае шарики двух наиболее редких цветов закончатся раньше, чем шарики одного наиболее популярного, если украшать каждый стол с использованием двух шариков наиболее популярного цвета.
, но только тогда, когда max(r, g, b) ≥ 2·(r + g + b - max(r, g, b)), в таком случае ответ r + g + b - max(r, g, b). В этом случае шарики двух наиболее редких цветов закончатся раньше, чем шарики одного наиболее популярного, если украшать каждый стол с использованием двух шариков наиболее популярного цвета.
Для начала можно заметить, что для того, чтобы построить красно-зеленую башню высоты h потребуется 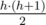 кубиков. Следовательно, высота полученной башни для заданных ограничений никогда не превысит 893. Эту высоту можно определить заранее, если предположить, что все кубики одного цвета. Попробуйте доказать это самостоятельно. Далее можно решить задачу с использованием динамического программирования. Пусть F(t, r) — количество способов собрать башню наибольшей высоты, если собрано t верхних этажей и остались незадействованными r красных кубиков. Среди аргументов функции нет количества оставшихся зеленых кубиков g — его можно однозначно определить из значений t и r:
кубиков. Следовательно, высота полученной башни для заданных ограничений никогда не превысит 893. Эту высоту можно определить заранее, если предположить, что все кубики одного цвета. Попробуйте доказать это самостоятельно. Далее можно решить задачу с использованием динамического программирования. Пусть F(t, r) — количество способов собрать башню наибольшей высоты, если собрано t верхних этажей и остались незадействованными r красных кубиков. Среди аргументов функции нет количества оставшихся зеленых кубиков g — его можно однозначно определить из значений t и r: 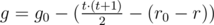 , где r0 и g0 — изначальное количество красных и зеленых кубиков, соответственно. Ну а дальше следует рассмотреть лишь два перехода: пострить t + 1-ый уровень из красных или из зеленых кубиков: F(t, r) = F(t + 1, r - t) + F(t + 1, r). Очевидно, кешировать данные в массиве размера 893 × 2·105 — не лучшая затея. В таком случае можно подсчитывать значения функции для всех значений t от 0 до h, храня в памяти только значения для текущего значения t и для предыдущего, от которого оно будет зависеть.
, где r0 и g0 — изначальное количество красных и зеленых кубиков, соответственно. Ну а дальше следует рассмотреть лишь два перехода: пострить t + 1-ый уровень из красных или из зеленых кубиков: F(t, r) = F(t + 1, r - t) + F(t + 1, r). Очевидно, кешировать данные в массиве размера 893 × 2·105 — не лучшая затея. В таком случае можно подсчитывать значения функции для всех значений t от 0 до h, храня в памяти только значения для текущего значения t и для предыдущего, от которого оно будет зависеть.
Для решения этой задачи необходимо было заметить, что волнистых чисел на интервале от 0 до 107 намного меньше, чем 107. В таком случае можно решить задачу с использованием подхода meet-in-the-middle. То есть отдельно решить эту задачу для первых семи цифр ответа, и для последних семи цифр ответа. Для этого потребуется отдельно сгенерировать все волнистые числа на интервале от 0 до 107, которые начинаются с возрастания двух соседних цифр, и аналогичные волнистые числа, которые начинаются с убывания двух соседних цифр. Дальше для каждой первой половины мы можем посчитать rl — ее остаток от деления на n и, затем, определить количество подходящих вторых половин, которые должны иметь остаток от деления равный 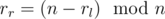 .
.
Для задачи было установлено ограничение времени равное 1.5 сек. На самом деле, если написать решение с подходом meet-in-the-middle достаточно оптимально, то решению потребуется гораздо меньше времени. Приведенная авторская реализация (8271836) умеет решать аналогичную задачу для 1 ≤ n, k ≤ 1016 примерно за 2.5 сек.











Where find English version
Note: English version of the above editorial.
478A — Starting bid
To solve the problem, it is important to note that during the game, the number of coins on the table can not be changed. The total number of coins on the table after a successful bid, remains unchanged. Therefore, by dividing the total number of coins on the table by the number of players, can obtain an initial rate for each. If you divide without remainder impossible, such a result can not play. Should pay attention to the fact that the initial rate of each of the players must be different from zero, hence, zero can never be the answer.
478B — Random team
If you restate the problem in terms of graph theory, it can be formulated as follows: There is a graph consisting of n vertices and m connected components. Inside each connected component, each pair of vertices connected by an edge of the component. In other words, each connected component is a full mesh. What is the smallest and the largest number of edges which may contain such a graph? Consider the process of constructing a graph of n vertices and m connected components. To begin, assume that each of the m component contains a single peak. It remains to distribute the remaining n — m vertices so as to minimize or maximize the number of edges. Note that when adding a new vertex in the connected component of size k, the number of edges is increased by k (new vertex is connected to each of the existing one edge). Consequently, in order to minimize the number of ribs formed on each step required each time to enhance top component connected smallest size. If you act according to this strategy, after the distribution of vertices on the connected components appears component size and component size. Similarly, in order to maximize the number of edges in each step must be added to the next vertex in the component connectivity greatest dimension. If you act according to such a strategy, then a single connected component of size n — m + 1, the remaining connected components will consist of a single vertex. Knowing the number of connected components and their sizes, you can count the total number of edges. For a full mesh components consisting of k vertices, the number of edges equals. It should be remembered about the need to use a 64-bit data type to store the number of edges, which depends quadratically on the value of n.
478C — table decoration
Consider a situation where the value max (r, g, b) — min (r, g, b) ≤ 1, then obviously the answer is (r+g+b)/3. We can always decorate so many tables three balloons of different colors. Obviously, the remaining amount will be less than three balls, and hence can not be used to decorate the table anyway. All the remaining cases it makes sense to reduce to the previously discussed. If there is one color, such that the number of balls that color is greater than the total number of balls for the other two colors, it is advantageous to decorate a table with two balls of one color and the ball of the remaining colors, which is greater than presently. Further it is possible in many ways to group operations and to carry out more than one operation at a time. Another solution include the fact that the response is different from (r+g+b)/3, but only if max (r, g, b) ≥ 2 · (r + g + b — max (r, g, b)), in which case the response r + g + b — max (r, g, b). In this case, the balls of the two most rare flowers will end earlier than the balls of one the most popular, if you decorate each table with two balls of the most popular colors.
478D — Red and green towers
To begin, you will notice that in order to build a red-green tower height h requires h(h+1)/2 cubes. Therefore, the height of the resulting tower predetermined limits never exceeds 893. This height can be determined in advance, if it is assumed that all blocks of the same color. Try to prove it yourself. Further it is possible to solve the problem using dynamic programming. Let F (t, r) — the number of ways to gather the greatest height of the tower, if collected t upper floors remained untapped r red cubes. Among the arguments of the function are no amounts remain green cubes g — can be uniquely determined from the values of t and r: g = g0 — (t(t+1)/2 — (r0-r)), where r0 and g0 — the initial number of red and green cubes, respectively. Well and further consideration should be given only two transitions: Build t + 1-th level of the red or green blocks: F (t, r) = F (t + 1, r — t) + F (t + 1, r). Obviously, the cache data in an array size of 893 × 2 × 105 — not the best idea. In such a case, you can count the value of the function for all values of t from 0 to h, stored in memory, only the values for the current value of t and the previous one, from which it will depend.
478E — Wavy number
To solve this problem, it was necessary to note that the numbers on the undulating range of from 0 to 107 is much smaller than 107. In this case, the problem can be solved using an approach meet-in-the-middle. That is separate to solve this problem for the first seven digits of the answer, and for the last seven digits of the answer. This will require the wavy separately generate all numbers in a range from 0 to 107, starting with the increase of two adjacent numbers and similar wavy numbers which begin with the decrease of two adjacent numbers. Then for each of the first half, we can calculate rl — its residue modulo n and then determine the appropriate amount of the second half, which should be equal to the remainder of the division rr = (n-rl)mod n.
For the problem was a limitation of time equal to 1.5 seconds. In fact, if we write the solution to the approach meet-in-the-middle optimally enough, then the solution will take much less time. The above author's implementation (8271836) can solve a similar problem for 1 ≤ n, k ≤ 1016 for about 2.5 seconds. Courtesy: Google Translate
I know it's an old post, but the solution for B can be done in O(1) time using maths:
Finding k_max: -The formula for finding the number of distinct pairs in a list of numbers goes like this: n * (n — 1) / 2 — where n is the length of the list. If we expand it, we get a quadratic equation: (n^2 — n) / 2. Quadratic equations grow exponentially, thus we can say that if we want the highest k_max, we want to make 1 team have as many participants as possible. We can do this by giving every team only 1 participant: 1 * (1 — 1) / 2 = 0, and all the remaining participants go to any 1 team, making the k_max as large as it can be. Final formula: (n — m + 1) * (n — m) / 2 — here we replace the original n with n — m + 1, which equates to taking away m — 1 participants for every team except 1, and if we subtract the amount of participants taken with the number of participants, we get: n — (m — 1) = n — m + 1, thus the formula returns k_max.
Finding k_min: -As we said in the previous example, the formula for finding the amount of distinct pairs in a list of numbers is quadratic, the lower number of participants in each team, lower k_min. Instead of bunching every single possible participant into 1 team, we now want to spread the participants as much as possible, so that we get the lowest possible k_min. Final formula: n / m * (n / m — 1) / 2 * (m — n % m) + (n / m + 1) * n / m / 2 * (n % m). This one is a bit more complicated so we will take it apart and analyze it bit by a bit. First off, let's see what n / m * (n / m — 1) / 2 * (m — n % m) does. In the formula '/' is floor division and '%' is modulus. If we replace n / m with n, we can see the resemblance to the original formula: n * (n — 1) / 2 * (m — n % m). We replace n with n / m, because n / m returns the amount of participants in each team if we spread them out as much as we can (it will miss out on a few participants which are extra, since it's floor division). This way we can calculate how many participants each team has. In the part of the formula, we also see (m — n % m) multiplier. The multiplier has 2 parts: m and n % m, m returns the number of teams, and n % m returns the number of participants who are extra. With the 1st part of the Final formula (which is n / m * (n / m — 1) / 2), we can see that we calculate the number of participants each team has, we want to multiply it by the number of teams m, but we only want to multiply it with teams which don't have the extra participant, so we subtract m with n % m -> m — n % m. The second part of the final formula goes like this: (n / m + 1) * n / m / 2 * (n % m). Firstly let's analyze (n / m + 1) * n / m / 2, here we can see that n from the original formula is replaced with n / m + 1. That's because we are also trying to see how many participants each team has with n / m, but we're also counting the extra participant so we add 1 -> n / m + 1. If we replace n / m + 1 with n, we get: n * (n — 1) / 2 * (n % m). The n % m part is the last piece of the puzzle. We multiply the amount of participants each team has (counting the extra participant) with n % m, because that returns the amount of extra participants, so each extra participant we add to a team to spread them out as much as possible.
Final formulas: k_max = (n — m + 1) * (n — m) / 2 k_min = n / m * (n / m — 1) / 2 * (m — n % m) + (n / m + 1) * n / m / 2 * (n % m)
In this Editorial, k_min = n / m * (n / m — 1) / 2 * (m — n % m) + (n / m + 1) * n / m / 2 * (n % m) This Formula show wrong on test 8 In this test k_min value is 1041665277780 and jury's answer is 1041664166668.
165410856
Its because of the operator precedence. The logic is same but the brackets doing the trick here, As in C++ * is calculated before /. The correct should be kmin = (((n/m — 1)*(n/m))/2) * (m — n%m) + (((n/m)*(n/m + 1))/2 )*(n%m)
And don't forget to use 64bit datatype.
Here my accepted solution 212267547
Can someone explain me tutorial of the D?
look at Accepted codes, everything becomes clear.
D, can somebody translate to understandable?
"Let F (t, r) — the number of ways to gather the greatest height of the tower, if collected t upper floors remained untapped r red cubes."
Can you explain D in simpler terms. The English editorial is quite difficult to understand
I didn't get the editorial of Problem C.Can anyone explain it in a simple way and including all the mathematical details?
Say given colors are (a,b,c) and a<=b<=c then if max(a,b,c) — min(a,b,c) <=1 that means
1) Either max(a,b,c) == min(a,b,c) => a = b = c and answer is a = (a+b+c)/3 2) Or (a,b,c) = (a, a, a+1) or (a, a+1, a+1), here total number of colors = 3a + 1 or 3a +2, hence total number of decorations can maximum be a which is (a+b+c)/3
Secondly consider the case where c > 2*(a+b), then it is clear that answer is (a+b) because we can create tables using (a, 0, 2a) + (0, b, 2b) number of decorations.
Editorial suggests that if a+b < c, then take (0, 1, 2) colors to create a decoration and continue, now we have (a, b-1, c-2), I didn't understand why would this lead to optimal strategy.
Say we know the answer for (a, b-1, c-2) which is (a+b-1+c-2)/3, now the answer for (a,b,c) will be (a+b-1+c-2)/3 + 1 which is (a+b+c)/3.
Now the only thing left is say we start at (x,x,x) or (x,x,x+1) or (x,x+1,x+1) can we reach (a,b,c) by just adding (1,1,1) or (0,1,2) or (0,2,1) or (1,0,2) or (1,2,0). If so since we know the answer for (x,x,x) which is x, and each step we add 1, we know the answer for (a,b,c) will be (a+b+c)/3.
Also what happens in the case when a+b>c? Can some one explain?
I found an interesting solution by Hasan0540 to check whether (a,b,c) can be used to form m decorations, but didn't understand
AkiLotus's solution describes a way of creating decorations, Not sure why this is the right way.
Can someone explain D in simpler terms. The English editorial is quite difficult to understand.
Simpler editorial for D. Red-Green Towers: (I hope)
Let $$$r_0$$$ and $$$g_0$$$ be the initial number of red and green blocks, respectively. Firstly, let us figure out how many levels can be formed using $$$r_0+g_0$$$ blocks. It is trivial to notice that to build $$$n$$$ levels requires $$$\frac{n(n+1)}{2}$$$ blocks. Thus, we need to find max $$$h$$$ such that $$$\frac{h(h+1)}{2} \le r_0+g_0$$$. We can do that by simple iteration due to the low constraints of $$$r_0$$$ and $$$g_0$$$.
Next, let us define $$$dp_i$$$ as the number of ways $$$i$$$ red cubes can be arranged into complete levels. By arranging into complete levels, I mean finding an arrangement such that all of the $$$i$$$ red cubes are used up in forming the levels. For example, 4 red cubes can be arranged in 2 ways such that it forms complete rows — [1,3] and [4]. Note that [1,2] is not a valid arrangement since we still have 1 leftover block.
$$$dp_i$$$ can be formulated as $$$dp_i=dp_i+dp_{i-j}$$$, where, $$$j$$$ is the current row that we are trying to build using red blocks.
Now that we have the maximum number of rows that we can build using $$$r_0+g_0$$$ blocks, $$$h$$$, and $$$dp_i$$$ such that $$$i$$$ red cubes can be arranged into valid levels, we can build our answer by iterating over all $$$r \le r_0$$$, and adding $$$dp_i$$$ into our answer if $$$i+g_0 \ge \frac{h(h+1)}{2}$$$. This means that we are using $$$r$$$ red blocks and $$$g$$$ green blocks ($$$g \le g_0$$$) to form $$$h$$$ levels. Or, in other words, $$$ans= \sum_\limits{r=max(0, \frac{h(h+1)}{2}-g_0)}^{r_0}dp_r$$$
Note that this works because we are using all $$$r$$$ blocks to form some unique combination of levels, and thus the rest of the levels are filled up by some $$$g$$$ green blocks, such that $$$r+g= \frac{h(h+1)}{2}$$$. Also you can compute $$$dp_i$$$ for green blocks instead of red, and it will work too.
C++ code.
PS: Sorry for necro-posting. I saw that there were a few requests for an explanation for problem D since the English editorial was a bit difficult to understand, thus I wrote this, just in case it helps.
nice explanation bro...
Video Solution for Problem C: https://www.youtube.com/watch?v=Pibw2uJQ7hA
assuming that r >= b >= c
when ``` ( b + c) *2 <= r ```` is not satisfied
neither
max ( r , b , c ) - min ( r , b , c ) <= 1satisfiedhow we ensure that taking ( a + b + c ) /3 cover the optimal way of choosing ?